동적 프로그래밍 조약돌 놓기 : 백준 9465번 스티커

조약돌 놓기 문제
1. 문제 설명
3행 n열 테이블의 각 칸에 정수가 기록되어 있다.
이 테이블에 조약돌을 놓는 방법 (제약 조건)은 다음과 같다.
- 각 열에는 적어도 하나의 조약돌을 놓아야 한다.
- 가로나 세로로 인접한 두 칸에 동시에 조약돌을 놓을 수 없다.
목표: 돌이 놓인 자리에 있는 수의 합이 최대가 되도록 조약돌을 놓기



* 4가지 패턴 임의의 열을 채울 수 있는 방법은 4가지 패턴뿐이다.
패턴 1
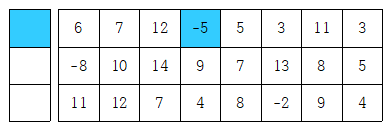
패턴 2

패턴 3

패턴 4

* 인접할 수 있는 패턴
패턴 1
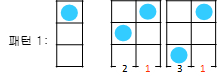
패턴 1은 패턴 2, 3과 인접할 수 있다.
패턴 2

패턴 2는 패턴 1, 3, 4과 인접할 수 있다.
패턴 3
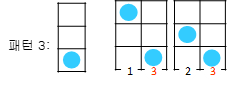
패턴 3은 패턴 1, 2과 인접할 수 있다.
패턴 4

패턴 4는 패턴 2와 인접할 수 있다.
* 인접할 수 없는 패턴
(패턴 1, 패턴 1)
(패턴 2, 패턴 2)
(패턴 3, 패턴 3)
(패턴 4, 패턴 4)
(패턴 1, 패턴 4)
(패턴 3, 패턴 4)
boolean possible(int p1, int p2) { // 패턴 첫번째와 패턴 두번째가 서로 인접 가능한지
if(p1 == p2) return false; // 동일한 패턴은 인접할 수 없다.
int[][] patterns = { {1, 4}, {3, 4}, {4, 1}, {4, 3} }; // 인접할 수 없는 패턴
for (int i = 0; i < patterns.length; i++)
if(p1 == patterns[i][0] && p2 == patterns[i][1])
return false;
return true;
}2. 계산 방법
c열에 p 패턴으로 돌을 놓을 때,
0열~ c열까지의 점수의 최댓값을 구하는 함수이다.
3. 재귀적 해법
scoreColumn(int c, int p)
c열에 p패턴으로 돌이 놓일 때, c열의 점수의 합
c값의 범위는 0 1 2... n-1
p값의 범위는 1, 2, 3, 4
int column(int c, int p){
switch(p){
case 1: return a[0][c];
case 2: return a[1][c];
case 3: return a[2][c];
case 4: return a[0][c] + a[2][c];
}
return 0;
}sum(int c, int previous)
c-1열에 previous 패턴으로 돌이 놓여있을 때,
c열부터 마지막 열까지 점수의 합 중 최대
previous 패턴으로 놓여있을 때 c열에 올 수 있는 패턴들에 대해서
sum(c+1, c열이 올 수 있는 패턴) 메서드를 재귀 호출하여 구현한다.
점수 = (위 메서드의 리턴 값) + (현재 열의 점수)
점수의 최댓값을 리턴한다.
int sum (int c, int previous) {
if(c >= a[0].length) return 0; // 종료조건
int max = Integer.MIN_VALUE;
for (int p = 1; p <= 4; p++){
if(c == 0 || possible(previous, p)){ // c 현재열이 0이면 이전 패턴과는 상관없다.
int score = column(c, p) + sum (c + 1, p);
if(score > max)
max = score;
}
}
return max;
}
4. 동적 프로그래밍으로 구현
int[][] dp = new int [4+1][a.length] // 행에는 이전 열의 패턴이 들어간다.
int sum (int c, int previous) {
if(c >= a[0].length) return 0; // 종료조건
if(dp[previous][c] != 0) return dp[previous][c]; // 이미 계산한 적이 있으면
int max = Integer.MIN_VALUE;
for (int p = 1; p <= 4; p++){
if(c == 0 || possible(previous, p)){ // c 현재열이 0이면 이전 패턴과는 상관없다.
int score = column(c, p) + sum (c + 1, p);
if(score > max)
max = score;
}
}
return dp[previous][c] = max;
}백준 9465번 스티커 설명
1. 문제 설명
2행 n열로 배치된 스티커를 뗄 때 스티커의 점수의 합이 최대가 되도록 스티커를 뗀다.
뗀 스티커의 왼쪽, 오른쪽, 위, 아래에 있는 스티커는 뗄 수 없다.
즉, 2 * n개의 스티커 중에서 점수의 합이 최대가 되면서 서로 변을 공유하지 않는 스티커 집합을 구해야 한다.
2. 문제 풀이
조약돌 문제와는 다른 점은 패턴은 3가지로 0행 스티커를 뗀 패턴, 1행 스티커를 뗀 패턴, 떼지 않은 패턴이다.
* 인접할 수 있는/없는 패턴
이전 열에서 아무것도 떼지 않았을 경우: 어떤 패턴이든 올 수 있다.
이전 열에서 0행이나 1행 스티커를 뗀 경우: 같은 행에 있는 스티커는 뗄 수 없다.
* 계속 아무것도 떼지 않을 경우
점수의 합이 0이 될 수 있다.
그렇기 때문에 dp를 -1로 초기화를 해주어야 한다.
마찬가지로, dp에 저장이 되어있는지 아닌지 확인할 때는 -1을 기준으로 검사해주어야 한다.
static int[][] dp;
static int sum(int[][] a, int c, int previous) {
if (c >= a[0].length)
return 0; // 종료조건
if (dp[c][previous] != -1)
return dp[c][previous];
int max = 0;
for (int r = 0; r <= 2; r++) {
if (r == 0 || r != previous) {
int ans = a[r][c] + sum(a, index + 1, r);
if (ans > max)
max = ans;
}
}
return dp[c][previous] = max;
}
jeon9825/TIP
✒️오늘 연습한 것을 정리하는 저장소✒️ Today I Practice . Contribute to jeon9825/TIP development by creating an account on GitHub.
github.com
'problem solving' 카테고리의 다른 글
| 동적프로그래밍/비트마스크/계단수 : 백준 10844번, 1562번 (0) | 2020.10.06 |
|---|---|
| 퀵 소트/ quick sort / quick select : 백준 11004번 문제 (2) | 2020.07.07 |
| 나머지 연산의 특징 : 백준 1629번 백준 13171번 (0) | 2020.04.28 |
| 우선순위 큐 : 백준 11279번 1927번 java (1) | 2020.04.27 |


댓글 개