1. 백준 10844번 쉬운 계단 수

2. 백준 1562번 계단 수

둘 다 동적 프로그래밍에 관한 내용이다. 

2번은 1번 문제에 하나의 조건만 추가되었다.

"0~9까지 모든 수를 한번 이상 사용해야 한다는 것이다." (길이가 N이면서 0에서 9가 모두 등장하는 계단 수가 총 몇 개?) 이 과정에서 비트 마스크가 사용된다.

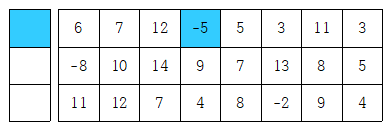
1번 백준 10844번 쉬운 계단 수 문제

i번째 자리의 수를 결정하고

i+1번째 자리의 수를 결정하는 부분을 재귀 호출한다.

앞자리 수가 결정되었을 때,

가능한 현재 자리 수는 앞자리수 - 1, 앞자리수 + 1 두 가지이다.

현재 자리 수는 0부터 9 사이의 숫자여야 하기 때문에

앞자리 수가 0일 때는, 현재 가능한 수는 1(앞자리수+1)뿐이고

앞자리 수가 9일 때는, 현재 가능한 수는 8(앞자리수-1)뿐이다.

종료 조건은 남은 자릿수가 0일 때 1을 리턴한다. (개수)

static int 계단수(int 길이, int 앞자리) { 
  if (길이 <= 0) // 종료 조건
    return 1; 
    
  int 결과 = 0; 
  
  if (앞자리 - 1 >= 0) 
    결과 += 계단수(길이 - 1, 앞자리 - 1); 
    
  if (앞자리 + 1 <= 9) 
    결과 += 계단수(길이 - 1, 앞자리 + 1); 
    
  return 결과; 
} 

static int solution(int N) { 
  int 결과 = 0; 
  for (int i = 1; i <= 9; ++i) 
    결과 += 계단수(N - 1, i); 
  return 결과; 
}

이는 O(2^N)의 시간 복잡도가 발생하여 "동적 프로그래밍"으로 시간 효율성을 높여야 한다.

결과 배열[길이][앞자리]를 저장하는 배열을 만들었다.

static final int M = 1000000000; 
static long[][] 결과배열; // 동적프로그래밍을 사용하기 위한 저장소

static long 계단수(int 길이, int 앞자리) {
  if (길이 <= 0) 
    return 1; 
    
  if (결과배열[길이][앞자리] > 0) 
    return 결과배열[길이][앞자리]; 
    
  long 결과 = 0; 
  if (앞자리 - 1 >= 0) 
  	결과 = (결과 + 계단수(길이 - 1, 앞자리 - 1)) % M; 
  if (앞자리 + 1 <= 9) 
  결과 = (결과 + 계단수(길이 - 1, 앞자리 + 1)) % M; 
  
  return 결과배열[길이][앞자리] = 결과; 
} 

static long solution(int N) { 
  long 결과 = 0; 
  for (int i = 1; i <= 9; ++i) 
    결과 = (결과 + 계단수(N - 1, i)) % M; 
  return 결과; 
}

2번 1562번 계단 수

모든 수를 사용해야 한다고 한다. 

보통 방문 여부를 결정할 때는 boolean으로 visited 여부를 결정한다.

하지만 이 문제에선 "비트 마스크"로 visited 여부를 결정한다.

비트 마스크는

방문하지 않았으면 0, 방문하였으면 1로 나타낸다.

만약

숫자 3이 방문하였으면 0000001000으로 표현하고

이는 1<<3으로도 표현할 수도 있다.

즉, 숫자 n이 방문하였으면 1<<n 으로 나타낸다.

숫자 5와 7이 방문하였으면 0010100000

숫자 0, 2, 9가 방문하였으면 1000000101

식으로 표현한다.

어떤 숫자를 방문한 상태에서 n을 방문할 경우

(방문한 상태를 나타내는 비트) | (1<<n)로 나타낸다.

즉 숫자 0과 9를 방문한 상태 비트는 (1000000001)이고

이 상태에서 숫자 2를 방문할 경우 (1000000101)

1000000001 | (1<<2)로 표현할 수 있다.

0부터 9까지 모든 숫자를 방문했을 경우

1111111111로 표현할 수 있고 (1<<10)-1로도 표현한다.

(아래에선 111111111으로 표현하지 않고 (1<<10)-1 로 나타냈다.)

모든 숫자가 방문했는지 여부를 확인하는 배열을 하나 추가해준다.

위의 코드에서 2차원 배열이었던 결과 배열을 3차원으로 변경해준다.

종료 조건은 남은 자릿수가 없을 경우 (길이가 0보다 작을 경우) 모든 숫자를 사용했는지 비트 마스크로 비교하였다.

비트가 (1<<10)-1과 같을 경우 1을 리턴

다를 경우 모든 숫자를 사용하지 않았으므로 0을 리턴한다.

현재 자리 수를 결정하고 나서 

비트도 변경해준다.

bit = 비트 | 1<< (앞자리-1)

bit = 비트 | 1<< (앞자리+1)

	static final int M = 1000000000;
	static long[][][] 결과배열;

	static long 계단수(int 길이, int 앞자리, int 비트) {
		if (길이 <= 0)
			return 비트 == (1 << 10) - 1 ? 1 : 0;

		if (결과배열[길이][앞자리][비트] > 0)
			return 결과배열[길이][앞자리][비트];

		long 결과 = 0;
		if (앞자리 - 1 >= 0) {
			int bit = 비트 | (1 << (앞자리 - 1));
			결과 = (결과 + 계단수(길이 - 1, 앞자리 - 1, bit)) % M;
		}
		if (앞자리 + 1 <= 9) {
			int bit = 비트 | (1 << (앞자리 + 1));
			결과 = (결과 + 계단수(길이 - 1, 앞자리 + 1, bit)) % M;
		}

		return 결과배열[길이][앞자리][비트] = 결과;
	}

	static long solution(int N) {
		결과배열 = new long[N][10][1 << 10];

		long 결과 = 0;
		for (int i = 1; i <= 9; ++i) {
			결과 += (계단수(N - 1, i, 1 << i) % M);
			결과 %= M;
		}
		return 결과;
	}

전체 코드 확인 백준 1562번 문제

백준 11004번 문제부터 얘기하자면 어렵지 않은 난이도인데 시간 초과로 계속 풀지못했던 문제

일단 학교에서 배운 quick sort와 quick select에 대해서 설명해보고자 한다.

1. quick sort (퀵 정렬)

1) 배열 나누기

임의의 값을 기준으로, 기준 값보다 작은 값들은 배열의 앞부분으로 이동하고, 기준 값보다 큰 값들은 배열의 뒷부분으로 이동하는 알고리즘.

기준 값: 입력 배열의 끝 값 (혹은 중간 값)

1구역: 기준 값보다 작거나 같은 값들이 위치할 곳

2구역: 기준 값보다 큰 값들이 위치할 곳

3구역: 아직 비교하지 않아서 위치가 정해지지 않은 값들

2) partition 구현

static void swap(int[] a, int i, int j) { 
  int temp = a[i];
  a[i] = a[j];
  a[j] = temp; 
} 
static int partition(int[] a, int start, int end) { 
  int value = a[end]; // 기준값 
  int i = start - 1; // i는 1구역의 끝지점
  for (int j = start; j <= end - 1; ++j) // j는 3구역의 시작 지점 
  if (a[j] < value) // a[j] 값이 1구역에 속하면 
    swap(a, ++i, j); // a[j] 값을 1구역의 끝에 추가한다. 1구역 크기 1증가. 
  swap(a, i + 1, end); // 기준값인 a[end] 원소와 2구역의 시작 원소를 교환한다. 
  return i + 1; // 기준값 위치 리턴 
}

3) 퀵 정렬 구현

static void quickSort(int[] a, int start, int end) {
  if (start >= end) 
    return; 
  int middle = partition(a, start, end); // 배열 나누기 
  quickSort(a, start, middle-1); // 1구역 정렬 
  quickSort(a, middle+1, end); // 2구역 정렬 
}

4) 퀵 정렬 수행 시간

partition 메서드의 수행시간은 O(n)이다.

평균

quickSort 메서드의 재귀 호출 횟수의 평균은 logn이다.

따라서 퀵정렬의 평균 수행시간은 O(nlogn)이다.

최선

partition 메서드가 배열을 정확히 1/2로 나눈다면, 재귀호출 횟수는 logn이고

따라서 퀵정렬의 최선일 때 수행시간은 O(nlogn)이다.

최악

partition 메서드가 배열을 0: n-1 크기로 나눈다면, 재귀호출 횟수는 n이다.

따라서 최악일 때, 퀵 정렬 수행시간은 O(n^2)이다.

=> 최악인 경우가 있기 때문에 기준값을 중간값으로 바꾸고 해보았지만 역시 시간 초과

2. quick select 

static void swap(int[] a, int i, int j) { 
  int temp = a[i]; 
  a[i] = a[j]; 
  a[j] = temp; 
} 

static int partition(int[] a, int left, int right) {
  int mid = (left + right) / 2;
  swap(a, mid, right);
  int pivot = a[right];

  int j = left - 1;
  for (int i = left; i < right; i++) {
    if (a[i] < pivot) {
		swap(a, i, ++j);
	}
  }
  j++;
  swap(a, right, j);
  return j;
}

// a 배열의 start~end 에서 nth 번째 작은 값을 리턴한다. 
static int select(int[] a, int start, int end, int nth) {
  if (start >= end) 
    return a[start]; // 찾을 배열의 크기가 1 이면 리턴 
  int middle = partition(a, start, end); // 배열 나누기 
  int middle_nth = middle - start + 1; // middle 위치의 값이 start~end 에서 middle_nth 번째 작은 값 
  if (nth == middle_nth) 
    return a[middle]; // 찾았으면 리턴 
  if (nth < middle_nth) 
    return select(a, start, middle-1, nth); // 앞 부분에서 찾는다.
  else 
    return select(a, middle+1, end, nth - middle_nth); // 뒷 부분에서 찾는다. 
}

근데 이렇게 해도 안된다. 대체 왜 (띠용)

partition 메소드에서 위 코드처럼 기준값을 중간값으로 바꿔줬는데도 시간초과가 뜬다.

3. 백준 11004번 문제

partition 메소드에 문제가 있는 것 같아서 아래의 메소드로 바꿨는데 시간초과가 뜨지 않는다.

사실 무슨 차이가 있는지 모르겠다. 암튼 아래 메소드로 바꾸니 됨...

(위 partition 메서드와 아래 partition 메소드의 차이점을 모르겠어요.. 아시는 분 댓글, 메일, 아무거나 부탁드립니다ㅜㅜ)

public static int partition(int[] array, int left, int right) {
	int mid = (left + right) / 2;
	swap(array, left, mid); // 중앙 값을 첫 번째 요소로 이동

	int pivot = array[left];
	int i = left, j = right;

	while (i < j) {
		while (pivot < array[j]) { // j는 오른쪽에서 왼쪽으로 피봇보다 작거나 같은 값을 찾는다.
			j--;
		}

		while (i < j && pivot >= array[i]) { // i는 왼쪽에서 오른쪽으로 피봇보다 큰 값을 찾는다.
			i++;
		}
		swap(array, i, j); // 찾은 i와 j를 교환
	}
	// 반복문을 벗어난 경우는 i와 j가 만난경우
	// 피봇과 교환
	array[left] = array[i];
	array[i] = pivot;
	return i;
}

전체 코드 확인 백준 11004번 문제 자바

조약돌 놓기 문제

1. 문제 설명

3행 n열 테이블의 각 칸에 정수가 기록되어 있다.

이 테이블에 조약돌을 놓는 방법 (제약 조건)은 다음과 같다.

- 각 열에는 적어도 하나의 조약돌을 놓아야 한다.

- 가로나 세로로 인접한 두 칸에 동시에 조약돌을 놓을 수 없다.

목표: 돌이 놓인 자리에 있는 수의 합이 최대가 되도록 조약돌을 놓기

* 4가지 패턴 임의의 열을 채울 수 있는 방법은 4가지 패턴뿐이다.

패턴 1

패턴 2

패턴 3

패턴 4

* 인접할 수 있는 패턴

패턴 1

패턴 1은 패턴 2, 3과 인접할 수 있다.

패턴 2

패턴 2는 패턴 1, 3, 4과 인접할 수 있다.

패턴 3

패턴 3은 패턴 1, 2과 인접할 수 있다.

패턴 4

패턴 4는 패턴 2와 인접할 수 있다.

* 인접할 수 없는 패턴

(패턴 1, 패턴 1)

(패턴 2, 패턴 2)

(패턴 3, 패턴 3)

(패턴 4, 패턴 4)

(패턴 1, 패턴 4)

(패턴 3, 패턴 4)

boolean possible(int p1, int p2) { // 패턴 첫번째와 패턴 두번째가 서로 인접 가능한지
	if(p1 == p2) return false; // 동일한 패턴은 인접할 수 없다.
    int[][] patterns = { {1, 4}, {3, 4}, {4, 1}, {4, 3} }; // 인접할 수 없는 패턴
    for (int i = 0; i < patterns.length; i++)
    	if(p1 == patterns[i][0] && p2 == patterns[i][1])
        	return false;
    return true;
}

2. 계산 방법

c열에 p 패턴으로 돌을 놓을 때,

0열~ c열까지의 점수의 최댓값을 구하는 함수이다.

3. 재귀적 해법

scoreColumn(int c, int p)

c열에 p패턴으로 돌이 놓일 때, c열의 점수의 합

c값의 범위는 0 1 2... n-1

p값의 범위는 1, 2, 3, 4

int column(int c, int p){
	switch(p){
    case 1: return a[0][c];
    case 2: return a[1][c];
    case 3: return a[2][c];
    case 4: return a[0][c] + a[2][c];
    }
    return 0;
}

sum(int c, int previous)

c-1열에 previous 패턴으로 돌이 놓여있을 때,

c열부터 마지막 열까지 점수의 합 중 최대

previous 패턴으로 놓여있을 때 c열에 올 수 있는 패턴들에 대해서

sum(c+1, c열이 올 수 있는 패턴) 메서드를 재귀 호출하여 구현한다.

점수 = (위 메서드의 리턴 값) + (현재 열의 점수)

점수의 최댓값을 리턴한다.

int sum (int c, int previous) {
	if(c >= a[0].length) return 0; // 종료조건
    int max = Integer.MIN_VALUE;
    for (int p = 1; p <= 4; p++){
    	if(c == 0 || possible(previous, p)){ // c 현재열이 0이면 이전 패턴과는 상관없다.
        	int score = column(c, p) + sum (c + 1, p); 
            if(score > max) 
            	max = score;
        }
    }
    return max;
}

4. 동적 프로그래밍으로 구현

int[][] dp = new int [4+1][a.length] // 행에는 이전 열의 패턴이 들어간다.
int sum (int c, int previous) {
	if(c >= a[0].length) return 0; // 종료조건
    if(dp[previous][c] != 0) return dp[previous][c]; // 이미 계산한 적이 있으면
    int max = Integer.MIN_VALUE;
    for (int p = 1; p <= 4; p++){
    	if(c == 0 || possible(previous, p)){ // c 현재열이 0이면 이전 패턴과는 상관없다.
        	int score = column(c, p) + sum (c + 1, p); 
            if(score > max) 
            	max = score;
        }
    }
    return dp[previous][c] = max;
}

백준 9465번 스티커 설명

1. 문제 설명

2행 n열로 배치된 스티커를 뗄 때 스티커의 점수의 합이 최대가 되도록 스티커를 뗀다.

뗀 스티커의 왼쪽, 오른쪽, 위, 아래에 있는 스티커는 뗄 수 없다. 

즉, 2 * n개의 스티커 중에서 점수의 합이 최대가 되면서 서로 변을 공유하지 않는 스티커 집합을 구해야 한다.

2. 문제 풀이

조약돌 문제와는 다른 점은 패턴은 3가지로 0행 스티커를 뗀 패턴, 1행 스티커를 뗀 패턴, 떼지 않은 패턴이다.

* 인접할 수 있는/없는 패턴

이전 열에서 아무것도 떼지 않았을 경우: 어떤 패턴이든 올 수 있다.

이전 열에서 0행이나 1행 스티커를 뗀 경우: 같은 행에 있는 스티커는 뗄 수 없다.

* 계속 아무것도 떼지 않을 경우

점수의 합이 0이 될 수 있다.

그렇기 때문에 dp를 -1로 초기화를 해주어야 한다.

마찬가지로, dp에 저장이 되어있는지 아닌지 확인할 때는 -1을 기준으로 검사해주어야 한다.

static int[][] dp;

static int sum(int[][] a, int c, int previous) {
	if (c >= a[0].length)
		return 0; // 종료조건
	if (dp[c][previous] != -1)
		return dp[c][previous];
	int max = 0;
	for (int r = 0; r <= 2; r++) {
		if (r == 0 || r != previous) {
			int ans = a[r][c] + sum(a, index + 1, r);
			if (ans > max)
				max = ans;
		}
	}
	return dp[c][previous] = max;
}

백준 9465번 스티커 코드

나머지 연산의 특징

나머지 연산은 기본적으로 결합, 분배, 교환법칙이 모두 성립하지 않는다. 그래서 사용할 때 계산순서와 위치를 주의해야 한다. 단, 나머지 연산에서 성립하는 독특한 법칙도 있다.

a를 b로 나눈 나머지 a mod b = a % b 라고 표현하기로 하자. 이 때 나머지는 다음과 같은 식들이 항상 성립한다.

( a + m ) % m = a % m

( a + b ) % m = ( ( a % m ) + ( b % m ) ) % m

증명) 

( a * b ) % m = ( ( a % m ) * ( b % m ) ) % m

증명) 

백준 1629번 문제

백준 13171번 문제

우선순위 큐 (Priority Queue)

일반적인 큐는 제일 먼저 들어간 데이터가 가장 먼저 나오게 되는 FIFO 자료 구조

우선순위 큐는 들어간 순서에 상관없이 일정한 규칙에 따라 우선순위를 선정하고, 우선순위가 가장 높은 데이터가 가장 먼저 나오게 됨.

사용하기

java에 내부적으로 구현되어 있다. 일반적인 큐처럼 add(); peek(); poll(); 등의 메소드를 사용할 수 있다.

PriorityQueue<Integer> pq = new PriorityQueue<>();

pq.add(4); //offer(); 메소드를 사용해도 동일하게 추가됩니다.
pq.add(3);
pq.add(2);
pq.add(1);

Integer poll = pq.poll();
System.out.println(poll); //출력결과 1

일반적인 큐와 다르게 가장 먼저 들어간 4가 아니라, 우선순위가 높은 1이 가장 먼저 들어감. 기본적으로는 낮은 숫자가 우선순위가 높습니다.

우선순위 변경하기

우선순위를 정하는 기준은 Java의 정렬 기준과 동일

Java는 기본적으로 낮은 숫자부터 큰 숫자로 오름차순으로 정렬하게 되는데, 다른 오름차순을 사용하고 싶다면 Comparator 클래스나 Comparable 인터페이스를 이용해야 한다.

Integer와 같은 숫자는 Collections.reverseOrder()를 사용하면 간편하게 우선순위를 변경할 수 있다.

//우선순위를 내림차순으로 변경
PriorityQueue<Integer> pq = new PriorityQueue<>(Collections.reverseOrder());

백준 11279번 문제

백준 1927번 문제

처음엔 백준 12279번과 1927번을 int 배열과 ArrayList<Integer>로 풀었는데 시간초과가 떴다. 문제가 있는 것 같아서 찾아보다가 우선순위 큐로 풀어야한다는 것을 배웠다. 우선순위 큐 말고 다른 방식으로 풀면 왜 시간초과가 뜨는지는 잘 모르겠다. 단순 java가 시간을 많이 잡아먹는게 문제인가